MONTY HALL PROBLEMİ

Matematik zordur dersem, herhalde çok şaşırtıcı bir şey söylemiş olmam. Soyutlanıp saf özüne indirilmiş düşünceyi evirip çevirmeyi öğrenmek çok çetin bir iştir. Tabii ki imkânsız değil. Ne de olsa dünyada onbinlerce profesyonel matematikçi var, ve başka insanlardan hiç farkları yok. Çalışınca her şey öğrenilir. Öte yandan matematikte öyle şeyler çıkabiliyor ki karşınıza, “uzmanım” diyenleri bile ters köşeye yatırabiliyor. Monty Hall problemi de masum görünen, ama adamı iki seksen yere yatırabilen bir olasılık problemi.

Podcast: Play in new window | Download

Subscribe: RSS

Problemin kaynağı bir yarışma programı. ABD televizyonlarında 1963’den 1977’ye kadar yayında kalan Let’s Make A Deal (Bir Anlaşma Yapalım) isimli programda sunucu Monty Hall konuklarla çeşitli oyunlar oynuyordu. Bu oyunların ortak özelliği, yarışmacıların küçük bir ödülü alıp gitmek veya riske girerek büyük bir ödül kazanmak (veya hiç bir şey almamak) arasında karar vermelerinin gerekmesiydi.

Monty Hall’un sunduğu oyunlardan birisi, 1975’de The American Statistician isimli akademik dergide Kaliforniya Üniversitesi, Berkeley’de çalışan matematikçi Steve Selvin tarafından bir olasılık problemi halinde sunuldu. Makalede Monty Hall Problemi olarak anılan bilmece şöyle:

Önünüzde üç tane kapalı kapı var. Bunlardan birinin arkasında son model bir otomobil, diğer ikisinin arkasında ise birer keçi var. Kapılardan birini seçiyorsunuz, ama henüz açılmıyor. Monty Hall hangi kapının arkasında araba olduğunu biliyor. Seçmediğiniz iki kapıdan birini açıyor ve o kapının arkasındaki keçiyi görüyorsunuz.

Monty Hall isterseniz tercihinizi değiştirip, açılmamış diğer kapıyı seçebileceğinizi söylüyor. Arabayı kazanma ihtimalinizi artırmak için ne yapmalısınız? Başka bir deyişle, tercihinizi değiştirmekle araba kazanma ihtimaliniz artar mı, azalır mı, yoksa hiç mi değişmez?

Bu problemi duyan çoğu kişinin, uzmanlar dahil, ilk tepkisi “Değişmez” demek. Başta doğru kapıyı seçme ihtimali ⅓ idi. Şimdi iki kapalı kapı var, ve oyuncunun seçtiği kapının arkasında araba bulunması ihtimali ½. Yani tercihi değiştirmek kazanma ihtimalini artırmayacaktır. Fakat işler o kadar basit değil; Monty’nin arabanın hangi kapı arkasında olduğunu bilmesi ve özellikle keçili kapıyı açıyor olması problemi değiştiriyor. Oyuncu için doğru strateji kapıyı değiştirmek. Nasılını sonraya bırakalım, böylece biraz düşünmeye zamanınız olsun.

Olasılık tuzakları

Monty Hall probleminin, ve genel olarak şans ve risk içeren bütün karar problemlerinin, kesin kazanç getiren stratejileri yok. Yapabileceğimiz tek şey kazanma ihtimalimizi mümkün olduğunca yükseltmeye çalışmak. Bu her zaman kolay değil, çünkü insan zihni için olasılıklarla düşünmek çok zor. Birçok kez, varsayımlarımız ve ön kabullerimiz bizi yanıltıyor.

Psikologlar olasılık problemlerinin algılanışı ve cevaplanmasıyla yakından ilgileniyorlar, çünkü bu konudaki düşünce tarzımız zihnimizin nasıl çalıştığına ve ne tür hatalara yatkın olduğuna ışık tutuyor.

En basitinden, şöyle bir soru düşünelim:

İki çocuğumdan biri erkek. Diğerinin de erkek olması ihtimali nedir?

Çoğu kişi gibi bu soruya %50 cevabını vermiş olabilirsiniz. Ne de olsa bir çocuğun cinsiyeti, ailenin diğer çocuğunun cinsiyetine bağlı değildir. Sorudaki ilk bilgi aslında gereksizdir, tuzağa düşmemiş olmanın haklı gururu ile gülümsersiniz.

Maalesef yanlış. Doğru cevap %33. Bunu görmek için durumları tek tek saymak gerekir. Erkek çocuğu E, kız çocuğu K ile gösterelim. İki çocuklu bir ailenin çocuklarının ikisi de erkek (EE), büyüğü erkek küçüğü kız (EK), büyüğü kız küçüğü erkek (KE), veya ikisi de kız (KK) olabilir. Soruda çocuklardan birinin erkek olduğu söylenmiş, yani mümkün olan durumlar sadece EE, EK, KE (“olay uzayı” diye de bilinir). Bunlardan da sadece birinde diğer çocuk erkek olduğuna göre, ihtimal ⅓, yani %33 olur.

Yani sorudaki bilgi şaşırtmaca değil, gerekli. İşin püf noktası, soruda erkek çocuğun büyük mü küçük mü olduğunun söylenmemiş olması. Eğer soru “İki çocuğum var, büyüğü erkek.” diye başlasaydı %50 cevabı doğru olurdu.

Şimdi, psikoloji araştırmalarında sıkça rastlanan bir probleme göz atalım.

Bir şapkada üç kart var. Birinin iki tarafı kırmızı (KK), birinin iki tarafı beyaz (BB), sonuncusunun ise bir tarafı kırmızı bir tarafı beyaz (KB). Gözlerimizi kapatarak şapkadan bir kart seçiyoruz ve masaya koyuyoruz. Gözlerimizi açtığımızda kartın yukarı bakan yüzünün kırmızı olduğunu görüyoruz. Kartın altta kalan yüzünün de kırmızı olması ihtimali nedir?

Bu soruya ezici çoğunluğun (yaklaşık yüzde yetmiş) cevabı %50’dir. BB kartının çekilmediği belli, o zaman masadaki kart ya KK ya da KB’dir. Rastgele çektiğimiz için ikisinin de ihtimali aynı olmalı.

Ancak doğru cevap %66. Önümüzde gördüğümüz yüz KK’nin iki kırmızı yüzünden biri olabilir, veya KB’nin tek kırmızı yüzüdür. Yani, diğer yüzün kırmızı olduğu iki durum varken, beyaz olduğu bir durum var. Bu yüzden aranan ihtimal ⅔ olur.

Her iki soruda da düşülen bilişsel hata aynı: Sezgilerimizle düşünüyor, ortaya çıkan gözlemin gerçekleşme ihtimalini hesaplamaya çalışıyoruz. Oysa, sorularda bize verilen bilginin mümkün durumların sayısını azalttığını hesaba katmak gerekiyor.

Kapıyı değiştirmek

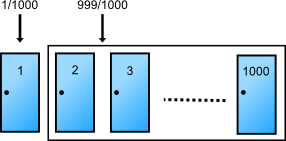
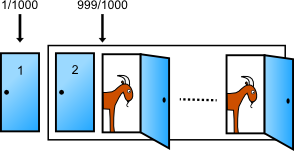
Monty Hall probleminde oyuncu için kapıyı değiştirmenin neden daha avantajlı olduğunu anlamak için oyunda üç değil, bin tane kapı olduğunu hayal edelim. Oyuncu yine kapılardan birini seçer. Binde bir ihtimalle araba seçtiği kapının arkasındadır, 999/1000 ihtimalle seçmediği bir kapının arkasında.

Monty oyuncunun seçtiği kapı haricindeki kapılardan 998 tanesini açar, hepsinin arkasında bir keçi olduğunu gösterir. Geriye iki kapalı kapı kalır: Oyuncunun seçtiği, ve Monty’nin kapalı bıraktığı.

Arabanın 999/1000 ihtimalle, seçilmeyen bir kapı arkasında olduğunu biliyoruz, ve açılmadık tek kapı kaldı. Yani oyuncu tercihini değiştirirse arabayı kazanma ihtimali birdenbire 999/1000’e yükselir.

Bin yerine üç kapı varsa, aynı akıl yürütmeyle oyuncunun arabayı kazanma şansı başta ⅓ iken, tercihini değiştirirse ⅔’e yükseleceğini görebiliriz. Kapıyı değiştirmek her zaman daha avantajlı.

İkna olmadıysanız, etkileşimli bir simülasyonu tekrar tekrar oynayarak her iki stratejinin ne sıklıkta kazandırdığını görebilirsiniz. “Let’s play”e tıklayıp oyunu başlatın. Üç kapalı kapıdan birine tıklayın. Bundan sonra “Continue”ya bastığınızda Monty arkasında keçi bulunan başka bir kapıyı açacak. Bu aşamada kapı tercihinizi değiştirmek (“Switch”) veya değiştirmemek (“Don’t switch”) kararı vereceksiniz. Kararınızdan sonra seçtiğiniz kapı açılacak. “Try Again” ile oyunu istediğiniz kadar tekrarlayabilirsiniz. Sağ taraftaki çizelgenin en altındaki “% Won” satırında, yaptığınız oyunlar arasında, karar değiştirerek ve değiştirmeyerek ne oranda başarı kazandığınızı görebilirsiniz. Oyun sayınız arttıkça (“Attempts”) bu oranlar yavaş yavaş %66.7 ve %33.3’e yaklaşacak. Tarayıcınız çerezleri kabul ediyorsa siteye daha sonra tekrar gittiğinizde kaldığınız yerden devam edebilirsiniz.

Kapı değiştirmenin kazanma garantisi demek olmadığına dikkat edin. “Kapıyı değiştirdim ama yine keçi çıktı!” diye şikâyet etmeyin, olabilir, şans bu. Şansa ve riske dayalı işlerde hiç bir strateji kazanma ihtimalini yüzde yüze çıkarmaz. Kazanma ihtimalinin ⅔ olması, mesela üç milyon kere bu oyunu oynasanız, tercihinizi değiştirdiğinizde yaklaşık iki milyon seferinde arabayı kazanabileceğiniz anlamına gelir.

Ters köşeye yatan uzmanlar

Steve Selvin Monty Hall probleminin şaşırtıcı çözümünü 1975’de yayınlamıştı, ama bu çözüm onbeş sene akademik kütüphane raflarında unutuldu. 1990’a gelindiğinde ana akım medyada ortaya çıktı. Ardından kopan fırtınayla Monty Hall problemi matematiğin unutulmuş köşelerinden çıkıp popüler kültürün bir parçası haline geldi.

Marilyn Vos Savant “dünyanın en zeki kadını” olarak bilinir. 190 IQ puanıyla “kadınlarda en yüksek IQ” kategorisinde Guinness Rekorlar Kitabı’na girmişti. (Kadın ve erkek IQ’larının ayrı sınıflandırılması eski önyargıların kalıntısı olsa gerek. Zaten Rekorlar Kitabı IQ kategorisini 1990’da kaldırdı).

Vos Savant 1986’da magazin dergisi Parade’de “Marilyn’e Sorun” isimli bir köşe yazmaya başladı. Okurlar merak ettikleri soruları gönderiyorlar, o da cevap yazıyordu. Soruların çoğu basit gündelik konularla ilgiliydi, ama arada bir akademik sayılabilecek sorular da geliyordu. 9 Eylül 1990 günü yayınlanan soru Monty Hall problemini tarif ediyordu. Vos Savant takdire şayan bir öngörü ile şu cevabı verdi.

Evet, tercihi değiştirmelisiniz. Birinci kapının kazanma şansı ⅓, ama ikinci kapının şansı ⅔. Olan biteni şöyle gözünüzde canlandırabilirsiniz: Varsayalım ki bir milyon kapı var ve siz 1 numaralı kapıyı seçtiniz. Kapıların arkasında ne olduğunu bilen ve ödüllü kapıya dokunmayan sunucu bütün kapıları açıyor, bir tek 777 777 numaralı kapıya dokunmuyor. Hemencecik o kapıya dönerdiniz, değil mi?

Sen misin böyle diyen! Parade dergisine binlerce eleştiri mektubu yağdı. Birçok matematikçi bu kadar “basit” bir meseleyi bile doğru bilemeyen magazin dergisi yazarını hizaya getirmek için seferber oldu. Matematikçilerin yazdığı mektuplardan biri şöyle:

Karıştırmışsınız! Açıklayayım. Bir kapının yanlış olduğu gösterildiğinde, bu bilgi geri kalan tercihlerin ihtimalini ½ değerine getirir, kapıların birinin diğerinden daha muhtemel olması için bir sebep yoktur. Profesyonel bir matematikçi olarak halkın matematik bilgisinin eksikliğinden çok rahatsızım. Lütfen hatanızı itiraf edin ve ileride daha dikkatli olun.

Başka biri:

Karıştırdınız, çok fena karıştırdınız! Buradaki temel ilkeyi kavramakta zorluk çeker gibisiniz, açıklayayım. Sunucu bir keçi gösterdikten sonra doğru seçim yapmış olma şansınız bire ikidir. Tercihinizi değiştirseniz de değiştirmeseniz de bu şans aynıdır. Bu ülkede yeterince matematik cahilliği var, ve dünyanın en yüksek IQ’sunun bunu yaygnlaştırmasına ihtiyacımız yok. Utanın!

Bu ve benzeri mektuplara cevaben Vos Savant biraz daha teknik bir çözüm yayınladı, ama bu da tartışmayı bitiremedi. Görünüşe göre koca koca matematikçiler bir magazin dergisi yazarının haklı olabileceğini kabul etmeye hazır değildiler.

1991 Şubat’ında Vos Savant aynı konuya tekrar değindi ve yine mektuplar yağdı.

Bir daha bu tipte bir soruya cevap vermeye yeltenmeden önce ihtimal hesabına dair bir ders kitabı edinmenizi tavsiye edebilir miyim?

Bir başkası:

Yarışma sorusu açıklamanız tamamen hatalı, umarım bu tartışma matematik eğitimindeki ciddi milli krizimize kamuoyunun dikkatini çekmeye yarar. Hatanızı kabul ederseniz rezil bir durumun çözümüne yapıcı bir katkınız olur. Fikrinizi değiştirmeniz için kaç kızgın matematikçi gerekli?

Bir diğeri:

Bir hata yaptınız, ama olaya olumlu açıdan bakın. Bütün bu doktoralılar hatalı olsalardı ülke çok ciddi bir derde batmış olurdu.

Sahi mi?

Öte yandan, bu problemin özellikle kafa karıştırıcı olduğunu da kabul etmek lâzım. Yirminci yüzyılın en büyük matematikçilerinden biri, ihtimal hesabı teorisini çok iyi bilen Paul Erdös bile, tercihi değiştirmenin kazanma ihtimalini artıracağını inatla reddetmiş, doğru çözümün ispatı gösterildiğinde bile fikrini değiştirmemişti. Ancak daha sonra bilgisayar simülasyonlarını görünce ikna oldu (muhtemelen o zamana kadar zihnini bu aykırı çözüme alıştırmıştı, yoksa simülasyonları da reddederdi).

Vos Savant cevabında sebat etti. Zamanla gelen tepkiler değişmeye başladı. Öğretmenler sınıflarında simülasyonlar yaptılar. Öğrencilerini iki gruba ayırdılar, grupların biri her zaman tercihini değiştirirken diğer grup hiç değiştirmedi.

Sekizinci sınıf öğrencilerimle teklif ettiğiniz deneyi yaptık. Teoriniz için bir denklem nasıl kurulabilir anlamıyorum, ama kesinlikle işe yarıyor. Olasılık kitaplarının tekrar yazılmasına katkıda bulunmanız gerekecek.

Los Alamos Laboratuarı’ndaki araştırmacılar aynı simülasyonu bilgisayarla yaptılar.

Los Alamos laboratuarında epeyce tartışma ve kararsızlık yaşadıktan sonra iki meslektaşı birbirlerinden ayrı olarak problemin programını yazdılar. Bir milyon deneme içinde, karar değiştirmek %66,7 oranında başarılı oldu.

Şamata dindiğinde Vos Savant’ın ününe yakışır bir öngörüye sahip olduğu teslim edilmişti. Monty Hall problemi akademik makalelerde etraflıca incelendi. Matematikçiler ve istatistikçiler, problemin çeşili varyasyonlarını analiz ettiler. Psikologlar ve bilişçiler insanların neden bu ve benzeri olasılık sorularında bu kadar zorluk çektiklerini sorguladılar. İktisatçılar bu problemdeki yanılgının iktisadi davranışa ve karar verme işlemlerine nasıl yansıdığını araştırdılar. Parade olayı ise, uzmanların da ara sıra yanılabileceğinin ispatı olarak matematik tarihine geçti.

Kaynaklar

• Jason Rosenhouse. The Monty Hall Problem. Oxford, 2009.
• Maya Bar-Hillel, Ruma Falk. Some teasers concerning conditional probabilities. Cognition, 11 (1982), 109-122.
• Wikipedia. The Monty Hall Problem.